本文提出了三維（三維）有限元分析(FEA)來預(yù)測微量潤滑(MQL)條件下深孔鉆的工件熱變形。鉆孔底表面(HBS)和孔壁表面(HWS)上的熱源首先采用逆?zhèn)鳠岱ù_定。開發(fā)了一種由攜帶HWS熱流的殼元素和攜帶HBS熱流的固體元素組成的三維熱載體，在鉆孔模擬過程中將熱傳導(dǎo)到工件。采用熱彈性耦合有限元分析，基于溫度分布計算了工件的熱變形。通過將溫度計算與現(xiàn)有的二維平流模型的比較，驗證了熱載體的概念。在連續(xù)鉆四個深孔的鋁工件上實(shí)驗驗證了三維熱畸變。在參考點(diǎn)上的測量失真為61lm，在不確定度范圍內(nèi)與FEA預(yù)測的失真為51lm相匹配。[DOI：10.1115/1.4005432]

1、    介紹

工件熱變形是精密加工過程中零件尺寸精度和質(zhì)量控制的關(guān)鍵。變形通常是由于工具-工件界面的熱傳導(dǎo)和工件表面[1]上高溫切屑的積累而導(dǎo)致的工件熱膨脹造成的。在低速或高縱橫比特征的干燥或準(zhǔn)干式（近干式）加工中工件熱膨脹明顯，如深孔鉆。關(guān)于精密加工中工件熱變形的有一些研究，但比較有限，例如斯蒂芬森等人研究了工件在干燥條件下硬車削時的熱膨脹，并報告了進(jìn)入工件的高熱通量流。Huang和Hoshi發(fā)現(xiàn)，由于工件的熱變形，低速面銑可能導(dǎo)致平整度差。在干式鉆孔中，由于鉆頭和工件上的熱膨脹，孔的幾何形狀通常逐漸變細(xì)，而入口直徑更小。

工件熱膨脹引起的問題在深孔微量潤滑(MQL)鉆孔中更為突出。MQL是一種接近干性的潤滑技術(shù)，它使用少量的潤滑劑與壓縮空氣混合，直接應(yīng)用在切割界面上，而不是用金屬切削液淹沒工件。雖然MQL提供同等或更好的潤滑，但它缺乏有效冷卻工件的能力。此外，MQL鉆孔中的高溫切屑可以在深孔鉆孔中的孔壁表面產(chǎn)生顯著的熱通量(HWS)。高HWS熱通量提高工件溫度，導(dǎo)致孔質(zhì)量更差。Tai等人對干式深孔和淺孔鉆孔的孔形進(jìn)行了研究已經(jīng)證實(shí)MQL深孔鉆孔中HWS的熱流量可以相當(dāng)于或大于HBS。在汽車動力總成精密MQL鉆孔中工件的熱變形已被觀察到足以導(dǎo)致后續(xù)加工操作中的位置誤差。多孔MQL鉆孔中工件熱變形引起的孔位置誤差研究尚不明確。

本研究建立了一個估算多個深孔MQL鉆孔過程中工件溫度和熱畸變的模型。利用基于工件溫度分布的熱彈性耦合有限元分析(FEA)對熱變形進(jìn)行了預(yù)測。對鉆孔過程中的工件溫度進(jìn)行了多項研究。弗萊舍爾等人測量了鉆孔后的穩(wěn)態(tài)工件溫度，以估計隨時間變化的平均表面熱通量。Bono和Ni建立了一個平流模型來計算和應(yīng)用HBS上的熱流?？ɡ_(dá)斯等人利用逆熱傳導(dǎo)法來確定從鉆點(diǎn)、唇部和邊緣到工件的與時間無關(guān)的熱流量。Tai等人采用逆?zhèn)鳠岱y定了MQL深孔鉆中HWS和HBS的隨時變化的熱通量。這種有限元分析適用于軸對稱工件上的單孔鉆孔建模。對于具有復(fù)雜幾何形狀和多個孔的工件，需要一個三維模型。采用平流方法進(jìn)行多孔鉆孔的三維熱彈性耦合有限元分析在技術(shù)上具有挑戰(zhàn)性，因為三維網(wǎng)格需要大量的計算時間，不斷去除工件材料和改變工件的幾何形狀。本研究提出了一種新型的利用載熱器的三維有限元分析模型來模擬不頻繁去除元件的工件加熱。

本文中，第二章首先介紹了該模型。第三章對該模型進(jìn)行了數(shù)值驗證。 第四章描述了模型驗證的實(shí)驗設(shè)置，第五章介紹了的熱建模和分析結(jié)果，第六章進(jìn)行了模型和結(jié)論的局限性討論。

2、    模型概念

工件的熱變形是由多孔鉆孔過程中工件的溫度變化決定的。模型概念包括三個部分：熱通定義、工件溫度計算工件和工件變形熱彈性耦合有限元。以下三節(jié)討論了在HWS和HBS上進(jìn)行深孔鉆孔時產(chǎn)生的熱通量、利用熱載體模型計算的工件溫度分布，以及由于多孔鉆孔引起的工件的熱變形。

2.1    深孔鉆孔中的熱通量

在深孔鉆孔有限元分析中，考慮了HBS上的h_b和HWS的h_w這兩個熱通量，如圖1中的二維軸對稱模型所示。平流模型用于計算鉆頭穿透工件時的工件溫度。它是通過在HBS上依次去除五層元素，并將h_b應(yīng)用到下一層來實(shí)現(xiàn)的。h_w隨平流過程一起應(yīng)用于HWS上。

根據(jù)恒定的鉆井進(jìn)給速率和速度，根據(jù)HBS假設(shè)h_b是與時間無關(guān)和均勻的。在鉆孔過程中，井面由于鉆頭深度的變化和芯片疏散條件而變化。如圖1(a)所示，h_w是HWS上的時間和軸向位置的函數(shù)。為了求解給定鉆孔條件下的h_b和h_w，采用了逆?zhèn)鳠岱椒?，該方法是基于由嵌入式熱電偶測量的溫度作為輸入。溫度測量需要一個與軸對稱平流模型對應(yīng)的圓柱形工件，如圖1(b)所示，其中熱電偶位于沿孔深度并靠近鉆孔表面。

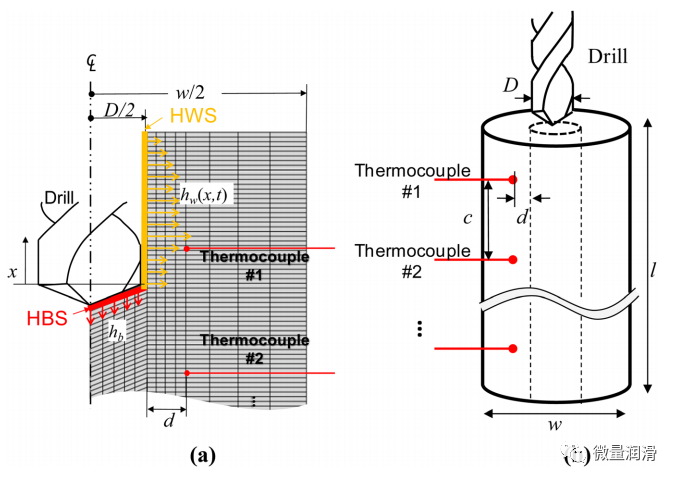
圖1.    (a)二維軸對稱平流有限元模型和(b)對應(yīng)的逆?zhèn)鳠岱椒ǖ膶?shí)驗設(shè)置

2.2    熱載波模型

熱載體模型是本研究開發(fā)的一個三維有限元分析模型，用來模擬深孔鉆孔過程中工件的溫度分布。如圖2(a)所示，熱載體施加恒定的h_b和隨時間變化的h_w（均由逆?zhèn)鳠岱椒ǐ@得），并進(jìn)入孔區(qū)，將熱量傳導(dǎo)到工件上。在鉆孔模擬之前，去除孔區(qū)域，以便熱載體可以進(jìn)入其中。這是基于軸向的傳熱通常比鉆孔進(jìn)給慢得多；因此，溫度分布不受熱載體進(jìn)入代表被鉆孔的空隙空間的顯著影響。該方法通過消除了去除三維元素的需要，克服了三維平流模型中的實(shí)際差異性。如圖2(b)三維平流模型的示意圖所示，圓柱形空穴區(qū)域被劃分為許多平流層區(qū)域。與二維平流模型1(a)不同，它在每個平流層上都有一個更簡單的網(wǎng)格模式，如果使用許多小的三維元素的薄層區(qū)域，元素的數(shù)量就會顯著增加。在形狀復(fù)雜的工件上鉆多個孔，每個孔需要大量的三維元件，需要大量的計算時間。熱載流模型如圖2.(a)所示簡化了三維有限元分析過程。

圖2.    (a)三維熱載流子模型和(b)三維平流模型的示意圖

如圖3(a)所示，由HWS和HBS載體組成的熱載體以鉆孔進(jìn)給速率移動，以模擬鉆井過程中對工件的熱傳導(dǎo)。由于熱載體和工件有不同的網(wǎng)格，孔表面不一致的網(wǎng)格尺寸可能會導(dǎo)致元件相互相交，導(dǎo)致有限元分析失效。因此，在孔的匹配表面和熱載體之間產(chǎn)生一個小的間隙，即鉆頭直徑的1%。為了使熱接觸電阻接近零的間隙傳熱，在ABAQUS（6.8版）中設(shè)置了相對較大的106W/m2K，這是本研究中使用的FEA軟件平臺。HWS和HBS熱載體的詳細(xì)信息。

2.2.1    HWS熱載體

HWS熱載體，如圖3(b)所示，是一個由四節(jié)點(diǎn)熱彈性耦合殼體元件組成的圓柱形殼體，在ABAQUS中為S4RT。這些元件沿著HWS載體被配置為許多環(huán)。HWS熱載體上軸向的環(huán)數(shù)為N，等于逆?zhèn)鳠岱ǖ钠搅髂Ｐ椭?span style="font-family: 宋體;font-size: 14px;">h_w的時間步長。HWS熱載體中每個環(huán)的軸向長度是平流模型中h_w在一個時間步長中移動的距離。對于環(huán)i(?1,2，...，N)，如圖3(b)所示，熱通量以h_w(xi，t)的大小均勻施加，其中xi是環(huán)i到HBS的中心位置，t是時間。當(dāng)HWS熱載體進(jìn)入孔時，每個環(huán)上的熱通量隨時間而變化。

2.2.2    HBS熱載體

HBS熱載體，如圖3(c)所示，是一個平行四邊形的橫截面圍繞著中心線，角度

θ是鉆點(diǎn)的角度。HBS熱載體由四節(jié)點(diǎn)四面體固體元素，ABAQUS中的C3D4T組成。在熱載體模型中，由于在應(yīng)用hb之前孔區(qū)被去除，因此不存在去除平流過程中存儲熱能的元件所造成的熱損失。在HBS載體上的修正熱流，表示為

h_b’提供了在平流模型中加熱工件的等效效應(yīng)。h_b’被描述為h_b乘以一個分配因子f，它在0和1之間，表示工件中沒有被平流過程去除的熱流量的比率。為了確定f，首先計算一個圓柱形工件的鉆孔過程吸熱總量，首先乘以三個參數(shù)：鉆孔后的穩(wěn)態(tài)工件溫度、帶鉆孔的工件質(zhì)量和工作材料的比熱。其次，利用逆?zhèn)鳠岱ǖ慕?，通過時間和空間分布對h_w(x，t)進(jìn)行積分，可以計算出通過HWS、HHWS流動的總熱量。分區(qū)因子f

其中，A為HBS的面積，t_f為總鉆孔時間。因此

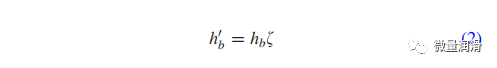
由于熱通過HBS熱載體的側(cè)面輸送到工件，即用圖中點(diǎn)EFGH所示的HBS熱載體的線GH標(biāo)記。適當(dāng)?shù)妮S向厚度(l_b)很重要。如果l_b太大，熱載體將儲存熱量，而不是將其傳導(dǎo)到工件上。如果l_b過小，則會影響HBS周圍溫度分布的精度。l_b根據(jù)指數(shù)p（以mm為單位）確定，其定義為

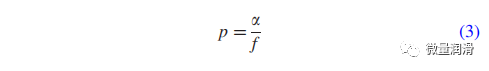
其中，α為工件的熱擴(kuò)散系數(shù)（mm/s2），f為鉆頭的軸向進(jìn)料速率（mm/s）。

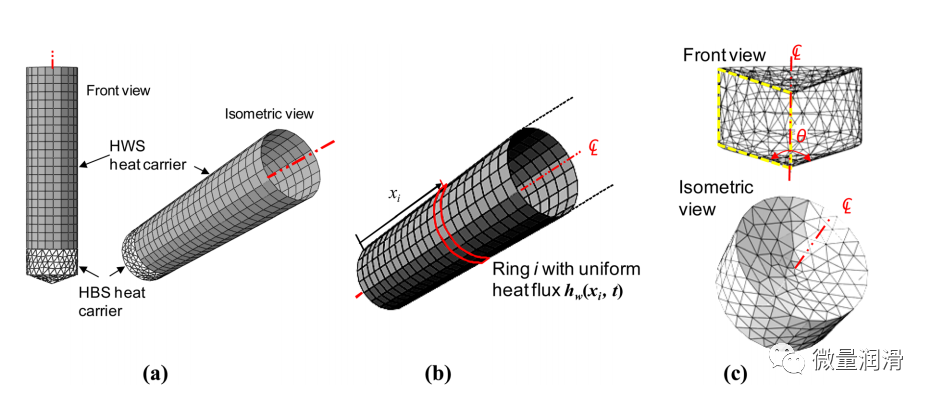
圖 3.    三維熱載體模型 (a)組裝了熱載體，(b)HWS熱載體，(c)HBS熱載體

p越大，意味著熱量可以在軸向上廣泛擴(kuò)散；因此，需要一個磅重較長的HBS熱載體。一般來說，在HBS熱流恒定的情況下，HBS周圍的溫度場收斂到一個特定的分布，如圖4所示，當(dāng)鉆孔超過一定深度時。因此，l_b和p之間的關(guān)系可以表示為lb?kp，其中k是一個常數(shù)比率，定義為

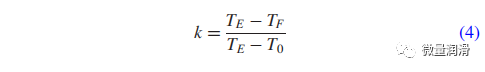
其中，T_E和T_F為E和F點(diǎn)的溫度，T₀分別為工件的初始溫度。k的最優(yōu)值是通過匹配二維軸對稱平流模型和HBS熱載流子模型的結(jié)果來確定的，如3.1章節(jié)中的示例。

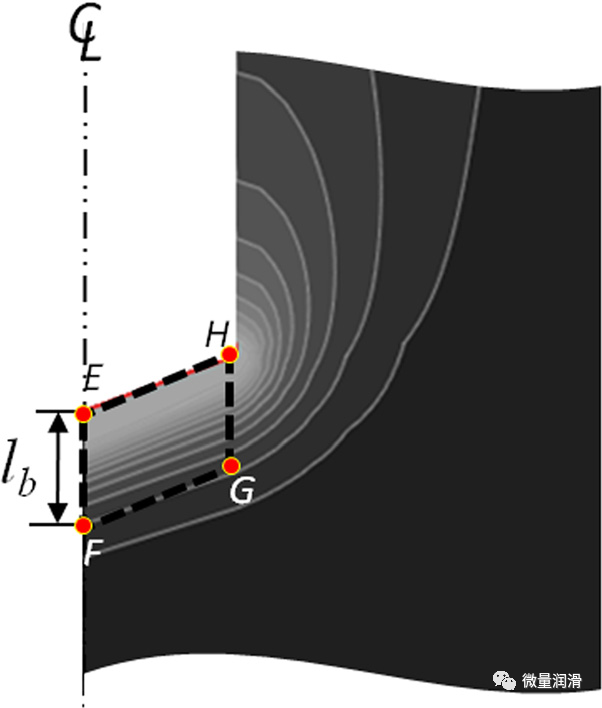
圖4.    軸向厚度(l_b)的定義，二維軸對稱HBS熱載體的幾何形狀(EFGH)，以及由于恒定的HBS熱流量引起的收斂溫度分布

2.3    多孔鉆孔中的工件熱畸變

利用有限元分析根據(jù)工件溫度預(yù)測多個深孔的工件熱變形。依次去除工件上的孔，并應(yīng)用熱載體將熱流輸送到工件。鉆孔后，主軸有一段時間可以收回并移動到下一個鉆孔位置。分析此期間的工件溫度，作為下一次鉆孔的初始條件。按順序鉆孔，溫度累積并輸送到工件中。例如，在分析開始時去除第一孔的區(qū)域，并將熱載體插入該孔中以進(jìn)行加熱。當(dāng)熱載體到達(dá)這個孔的末端后，工件中的熱傳遞繼續(xù)進(jìn)行開始進(jìn)行第二個鉆孔所需的一段時間。然后去除第二個孔的區(qū)域，用相同的熱通量插入熱載體。在后續(xù)鉆孔中重復(fù)此步驟。

為了預(yù)測熱變形，采用單獨(dú)的熱彈性有限元來避免同時求解位移和溫度，這在三維有限元中需要大量的計算時間。此外，工件的膨脹會產(chǎn)生與熱載體的接觸，并造成計算誤差。該方法首先計算了特定時間的工件溫度分布。提取該溫度場并導(dǎo)入熱彈性有限元分析，解決工件的熱變形問題。

3、    數(shù)值驗證

利用二維平流模型對計算得到的工件溫度與現(xiàn)有解進(jìn)行比較，對熱載體模型進(jìn)行了數(shù)值驗證。選擇的案例是沿著直徑40毫米的固體圓柱形球墨鑄鐵工件的中心線鉆一個直徑10毫米、200毫米深的孔。通過在平流模型中應(yīng)用熱流量h_b（?3.10MW/m2）和h_w（x、t），可以解決穩(wěn)態(tài)工件溫度。由此，計算出了HT?7.89kJ和HHWS?2.20kJ。使用公式。（1）與t_f=50s，f=48%和h_b’=1.49MW/m2。

驗證包括兩部分：一個驗證HBS熱載體模型和l_b(章節(jié)3.1)另一個則比較了使用二維平流模型和三維熱載體模型預(yù)測的工件溫度的差異（章節(jié)3.2）。

3.1    HBS熱載體模型驗證

為了找到軸向厚度(l_b)的最佳k，并驗證修正的熱流量(h_b’)，一個由三維HBS熱載體轉(zhuǎn)換而來的二維軸對稱HBS熱載體。3(c)]只應(yīng)用h_b’，與僅應(yīng)用h_b的2D平流模型進(jìn)行比較。該模型有140度的點(diǎn)角和直徑為10mm的孔（本研究中使用的鉆頭）。根據(jù)工材和鉆孔進(jìn)給率，可以確定p，在給定的k值下計算l_b，如第2.2.2節(jié)所述。最優(yōu)k從80%、70%、60%和50%四個值中選擇，間隔為10%，因為k對工件的整體溫度沒有顯著影響。對于球墨鑄鐵工件和4mm/s進(jìn)給速率，α為6.89mm2/s，p為1.72mm。圖5(a)和5(b)分別顯示了二維平流模式下和k?60%(磅?1.6mm)熱載體模型下100mm鉆井深度下的溫度分布。溫度分布為16毫米寬的8毫米在圖中突出顯示的區(qū)域。圖中覆蓋5(a)和5(b)。5個(c)，以供比較。k=60%的R²（0.97）更好。通過測試不同p下的k值（根據(jù)進(jìn)料特性或材料性能調(diào)整）下的k值，也發(fā)現(xiàn)最優(yōu)k為50%或60%。本研究選擇k=60%尋找l_b。

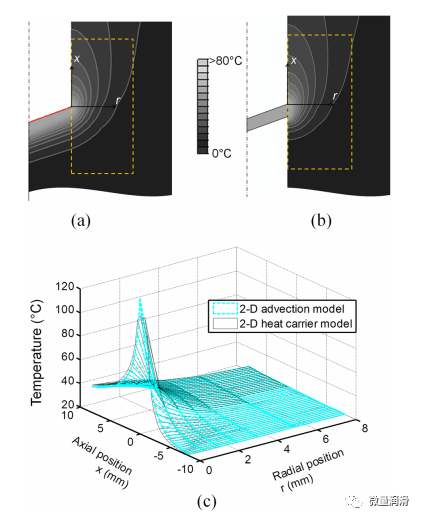
圖 5. 在HBS周圍的溫度分布， (a)二維平流模型， (b)為k5 60%的二維HBS熱載流子，(c)在(a)和(b)突出區(qū)域的溫度結(jié)果比較

覆蓋不同工作材料的廣泛進(jìn)料速率，如圖6所示,平流模型采用p=0.4mm~13.7mm的6例，根據(jù)溫度分布和k=60%尋找相應(yīng)的l_b。該范圍包括0.5至16mm/s進(jìn)料速率的鐵和5.5至150mm/s進(jìn)料速率的鋁的鉆孔條件。因此，l_b可以從圖6中得到。使用給定的工作材料和特定類型鉆孔的鉆孔進(jìn)料率。

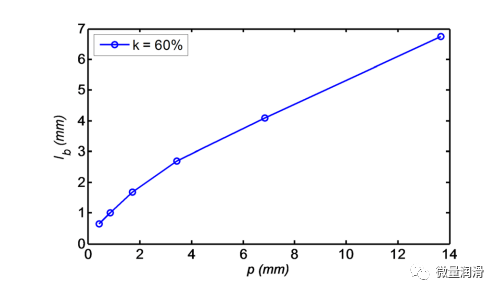
圖6.    由指數(shù)p確定的l_b范圍為0.4~13.7mm，k= 60%

3.2    三維載熱器模型驗證

組裝好的熱載體。圖3(a)]應(yīng)用于一個圓柱形的三維有限元分析用工件模型計算選定位置的溫度，并與二維平流建模結(jié)果進(jìn)行比較。對于三維HBS熱載體，其尺寸和形狀對應(yīng)于上一節(jié)中的二維軸對稱HBS熱載體，l_b=1.6mm。對于HWS熱載體，在200毫米長的圓柱形外殼上有125個環(huán)。該模型的初始溫度設(shè)置為20 ⁰C。圖7(a)顯示了使用三維熱載體模型在24.8s(=99.2mm鉆孔深度)時的工件表面溫度。表面溫度更高約30⁰C在上表面50mm處，。如圖7(b)所示，選擇5個距離HWS3.4mm且沿軸向長度定位的點(diǎn)，比較兩種模型預(yù)測的溫度和時間。如圖7(b)所示，最大差異約為峰值溫度5%，在鉆孔結(jié)束時，三維熱載體和二維平流模型的五個點(diǎn)的平均溫度分別為31.3⁰C和31.9⁰C。總的來說，兩種模型的結(jié)果一致，驗證了所提出的三維熱載體模型。

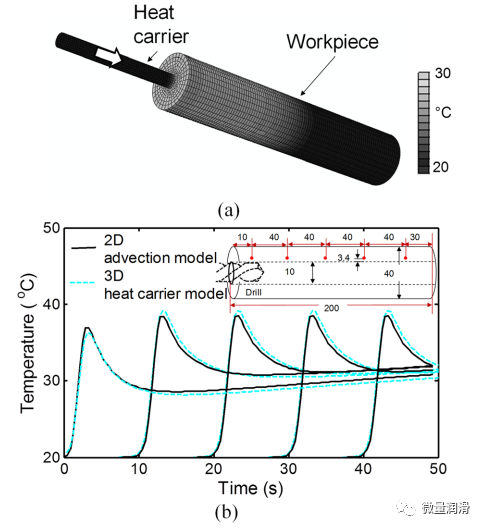
圖7.    (a)三維熱載體模型中24.8s鉆孔時間下的表面溫度，(b)三維熱載體模型與二維平流模型的溫度比較

4、    實(shí)驗設(shè)置

深孔鉆孔實(shí)驗是在一個Fadal垂直加工中心(VMC4020型)上進(jìn)行的。進(jìn)料速率和主軸轉(zhuǎn)速分別設(shè)置為0.2mm/rev和2100rpm。采用一種直徑10mm、長220mm、帶進(jìn)油孔的實(shí)心硬質(zhì)合金鉆頭(Titex，型號A6785TFP-10)。使用MQL輸送潤滑劑和空氣混合物。MQL系統(tǒng)的壓縮空氣供應(yīng)被調(diào)節(jié)到500kPa(5bar)。MQL潤滑劑為米拉克龍無鉻VG-703ES。流量約為60mL/h，主軸轉(zhuǎn)速為2100轉(zhuǎn)/分。

本研究選擇鋁6061-T6作為工作材料。本研究共進(jìn)行了兩組實(shí)驗。第一個，裝置I，是鉆孔一個圓柱形工件，用于熱通量h_b和h_w的逆?zhèn)鳠崛芤?。第二個是裝置II，用來驗證三維熱載體模型預(yù)測的熱畸變。

4.1    設(shè)置I：鉆井熱液的測定

圖8顯示了用于尋找HBS和HWS熱通量的設(shè)置I。圓柱形工件直徑38毫米，長152毫米。5根導(dǎo)線直徑為0.127mm的E型熱電偶(omega5型TCTT-E-36-72)嵌入在工件中，距離HWS3.4mm，彼此相距30mm。這些熱電偶在圖中分別標(biāo)記為TC1、TC2、TC3、TC4、TC5。8.選擇到HWS的3.4mm距離是為了避免在HWS附近的大溫度梯度，這可能會導(dǎo)致測量誤差，影響熱流估計的精度。熱電偶孔直徑為1.2mm，并填充熱膏，以減少熱接觸電阻。在MQL條件下，使用直徑10mm的碳質(zhì)物鉆在工件中心鉆一個直徑10mm的穿孔。總鉆孔時間為21.7s。這些溫度是以10hz的采樣率記錄下來的。

圖8.    設(shè)置I：采用逆?zhèn)鳠岱?/p>

4.2    設(shè)置II-工件熱失真

圖9(a)顯示了裝置II中的工件的形狀和尺寸，用于測量四個深孔的MQL鉆孔后的工件的熱膨脹。裝置II的實(shí)驗設(shè)置圖如圖9(b)所示工件是一個50.8毫米x152毫米x152毫米鋁塊，25.4毫米深，25.4毫米寬的區(qū)域伸出底部的一側(cè)夾緊。該設(shè)計旨在避免對工件在x方向上的熱膨脹引入重大約束[如圖9(a)所示]在鉆孔期間。XYZ坐標(biāo)系的原點(diǎn)設(shè)置在頂表面的角[圖9(a)中O點(diǎn)]。

四個152毫米深的通孔，在圖9(a)中標(biāo)記為#1、#2、#3和#4。使用相同的鉆頭、主軸速度和進(jìn)料速率按順序鉆入工件。4個淺層參考孔，標(biāo)記為a、b、c和d，用9.5mm的鉆頭鉆出了18mm深。孔a和孔b是在鉆四個深孔之前鉆出來的。c孔和d孔是在鉆了四個深洞后立即鉆孔的。孔a和b與孔c和d之間的x方向距離差以及編程的標(biāo)稱x位置[圖9(a)中127.0mm]。在機(jī)器中決定了通過實(shí)驗測量到的工件的熱膨脹。將實(shí)驗測量值與三維熱載流模型預(yù)測的x向熱膨脹進(jìn)行了比較。

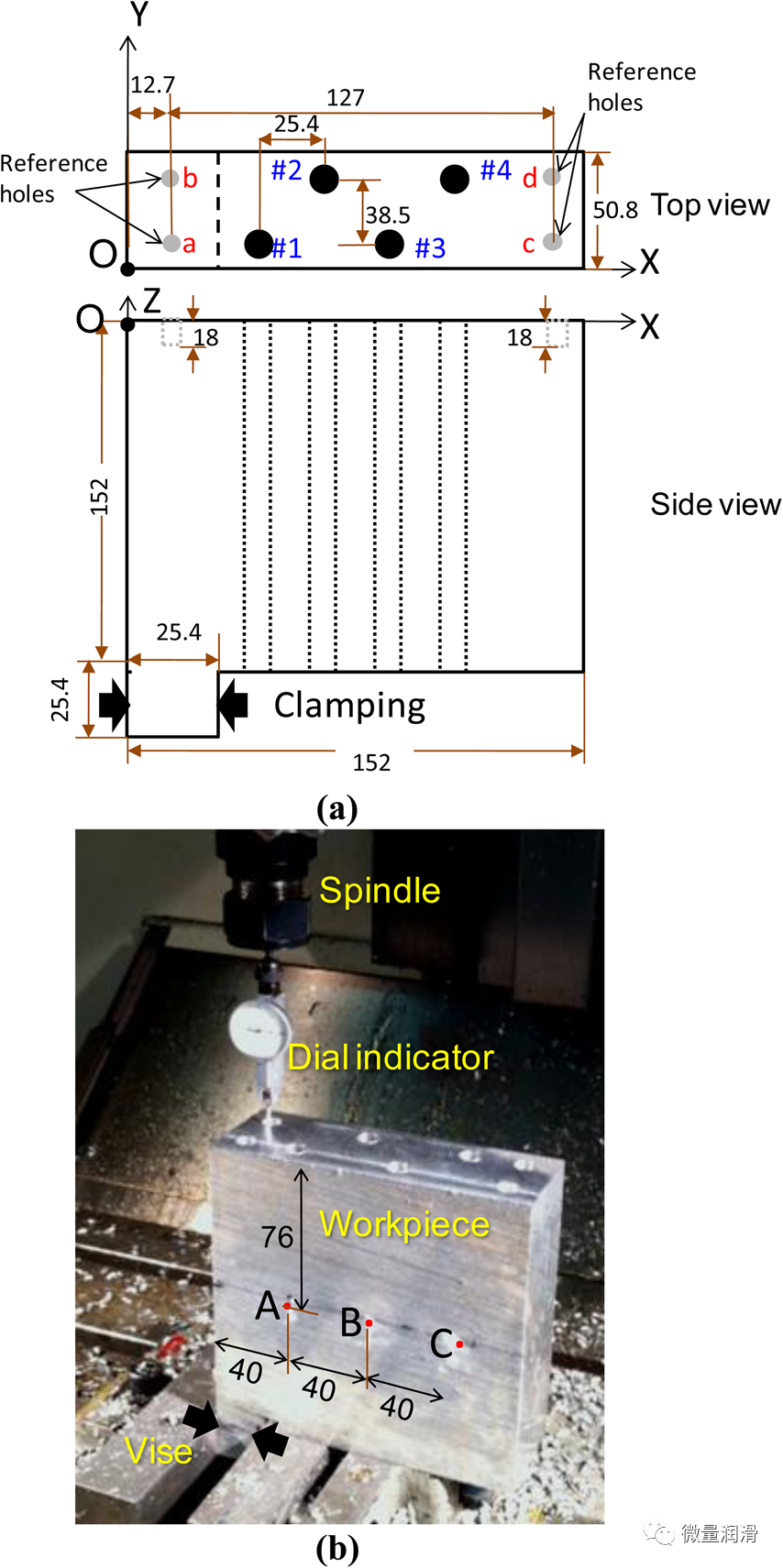
圖9.    設(shè)置II：(a)熱變形實(shí)驗工作臺面設(shè)計，(b)使用表盤指示器測量孔洞位置（單位：mm）

使用機(jī)器主軸上的表盤指示器測量參考孔的位置，如圖9(b)所示。將工件冷卻至室溫后。用Renishow激光干涉儀(ML10型)測量了機(jī)器在X軸上的定位精度。機(jī)器軸分辨率為2lm。激光干涉測量結(jié)果顯示，機(jī)器的X軸位置誤差低于5lm。表盤指示器的分辨率也在5lm以下。機(jī)器中使用表盤指示器的孔穴位置測量誤差估計小于10lm。

為了驗證有限元分析中的工件溫度，有三個熱電偶，分別標(biāo)記為A、B、C，如圖所示。9(b)，附著在工件表面上，用于測量鉆孔過程中的表面溫度。

5.    建模和實(shí)驗結(jié)果

介紹h_b和h_w的逆?zhèn)鳠峤?，介紹工件溫度，介紹工件熱變形。

5.1    HBS和HWS上的熱通量（設(shè)置I）

利用在五個熱電偶下的測量溫度。圖10(a)采用熱逆?zhèn)鳠岱y定熱通量。計算出的h_b為4.5MW/m2。h_w，作為時間和鉆位的函數(shù)，如圖10(b)所示。利用二維平流模型中的熱通量，將5個熱電偶位置的計算溫度與圖中的測量數(shù)據(jù)進(jìn)行了比較。有限元分析與測量溫度之間的良好一致性驗證了鋁的逆?zhèn)鳠岱椒?，這是一種新的工作材料，在我們之前的研究中沒有測試過。TC1在鉆孔早期（2~5s）存在一定差異。這種現(xiàn)象已在參考文獻(xiàn)中觀察到。是由于在逆熱中，熱模型無法捕獲的快速熱流變化轉(zhuǎn)移法本試驗在相同的鉆井條件下進(jìn)行了兩次試驗，溫度數(shù)據(jù)具有可重復(fù)性。

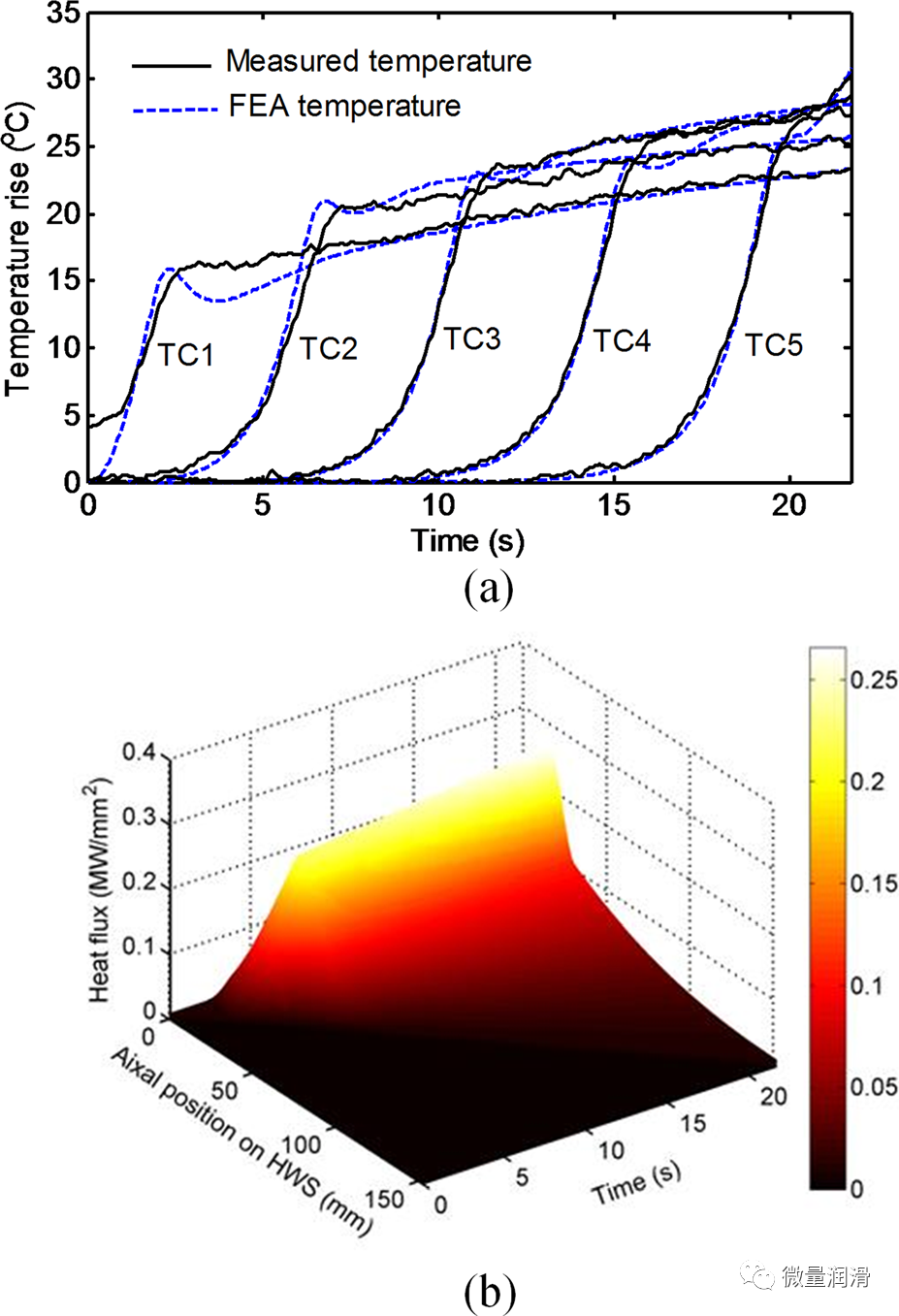
圖10.    逆?zhèn)鳠岱ǖ慕Y(jié)果：(a)測量和有限元計算了熱偶位置的溫度和(b)h_w的時空分布

5.2    工件溫度（設(shè)置II）

采用了三維熱載體模型。對于HBS熱載體，鋁6061的擴(kuò)散系數(shù)為74.4mm2/s，鉆孔進(jìn)給速率為7mm/s，因此，指數(shù)p為10.6mm。根據(jù)圖中示。k=60%，HBS載體厚度l_b為5.6mm。分配因子為0.82，因此h_b’為3.7MW/m2。對于HWS熱載體，沿著152毫米的長度創(chuàng)建了100個環(huán)(N?100)。這對應(yīng)于1.52mm的環(huán)軸向長度，比第二秒中的驗證案例(1.6mm)更好。3.隨時間變化的h_w[圖]。10(b)]采用逆?zhèn)鳠岱ㄓ嬎恪?/p>

圖11.    多孔鉆孔工件的三維有限元網(wǎng)格

將熱載體插入1孔之前工件的三維有限元網(wǎng)格如圖所示。11.第1號孔的區(qū)域已被刪除。熱載體。3(a)]移動速度為7mm/s（鉆頭的供給速率）進(jìn)入孔，以將熱流（hw和hb0）引入工件。圖12(a)為1孔熱載體穿透工件底部時的表面溫度分布。更高溫度接近工件的底部，靠近1號孔。在收回鉆機(jī)并移動到2號孔的位置時進(jìn)行了6.5s后，工件內(nèi)的溫度分布如圖12(b)所示，這也是2號鉆孔的初始工件溫度。然后去除2號孔的區(qū)域，將工件重新劃分，并插入熱載體以傳遞熱流。2號鉆孔后的工件溫度如圖12(c)所示。3、4號鉆孔后的工件溫度如圖所示。分別為12個(d)和12個(e)。在圖中可見的較高的溫度區(qū)域。12(d)是由于3號孔靠近工件的前表面。隨著鉆孔按順序進(jìn)行，可以觀察到工件整體溫度的逐漸增加。

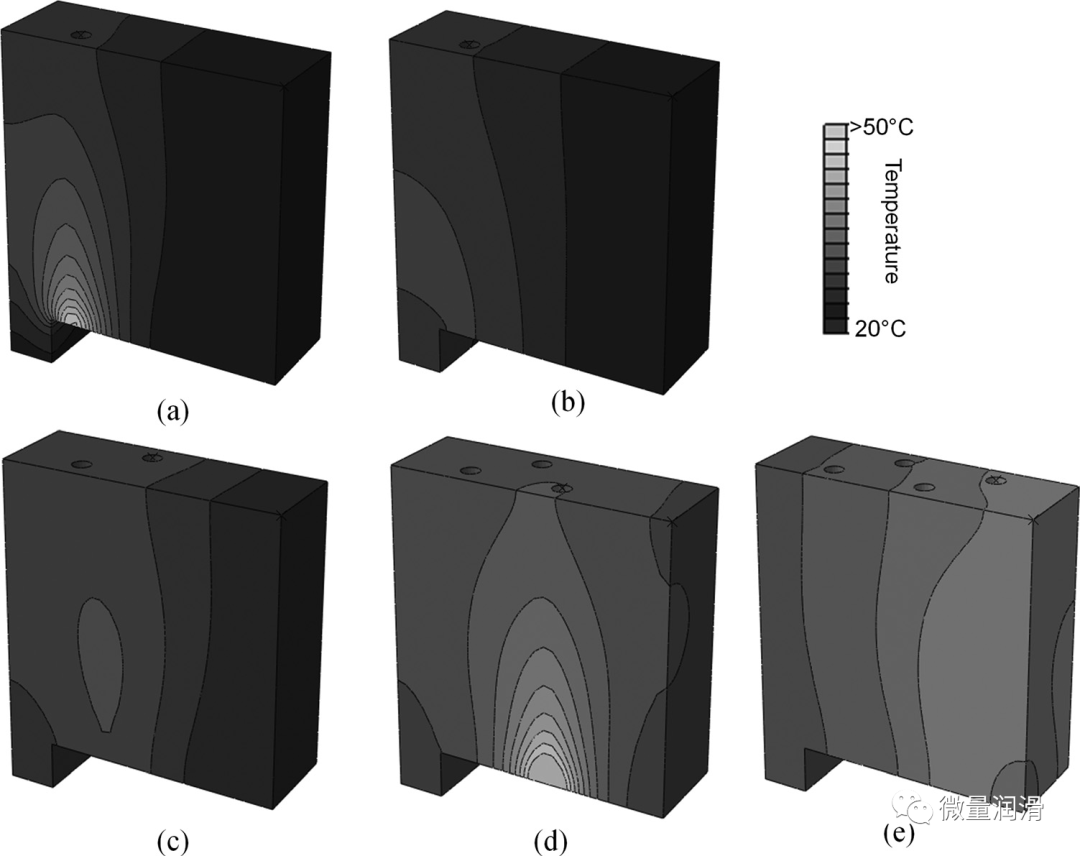
圖12.    1號鉆孔端(a)、1號鉆孔端后(b)6.5s、(c)號鉆孔2、3號(d)孔、(e)4號鉆孔端的工件溫度分布

A、B和C點(diǎn)的溫度。9)從有限元分析中提取，并與實(shí)驗測量結(jié)果進(jìn)行比較。作為如圖13所示。除了在A點(diǎn)和B點(diǎn)的峰值附近外，這些溫度非常匹配。進(jìn)一步的研究表明，這種差異是由于靠近鉆頭的高溫空間分辨率的限制。

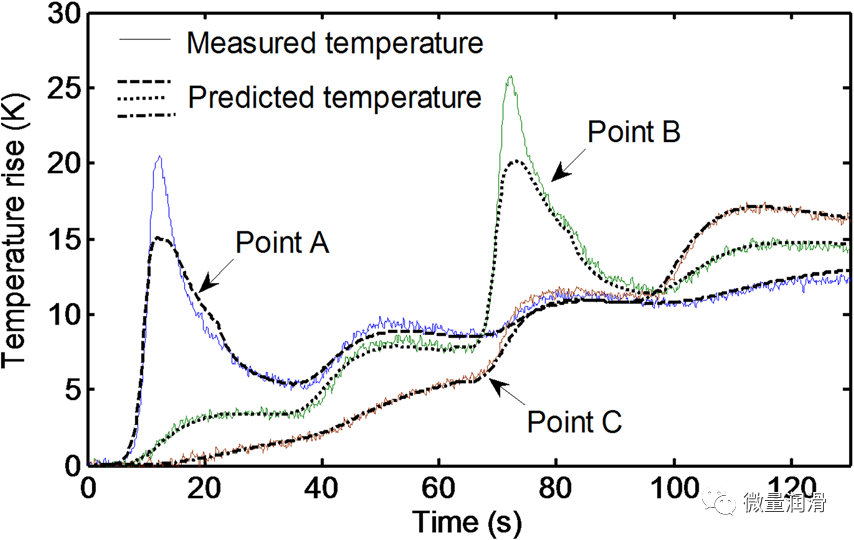
圖13.    測量和預(yù)測了A、B和C點(diǎn)的表面溫度

參考孔c、d更換刀具和定位鉆孔的時間延遲22s后，工件溫度分布如圖所示。工件兩側(cè)的14號。這是用于計算工件熱變形的溫度。工件底部角落的峰值溫度約為37.5⁰C?？拷?號孔的低溫為31.5⁰C，沿x方向觀察到溫度梯度。

5.3    工件失真（設(shè)置II）

圖中的溫度分布。將14改為8節(jié)點(diǎn)線性磚構(gòu)件(ABAQUS中的C3D8R)，采用熱彈性有限元分析模擬工件的熱膨脹。根據(jù)有限元分析預(yù)測的工件在x向上的熱膨脹情況如圖15所示，其中輪廓表示在x方向上的位移。橫跨YZ平面的工件熱變形幾乎是均勻的。

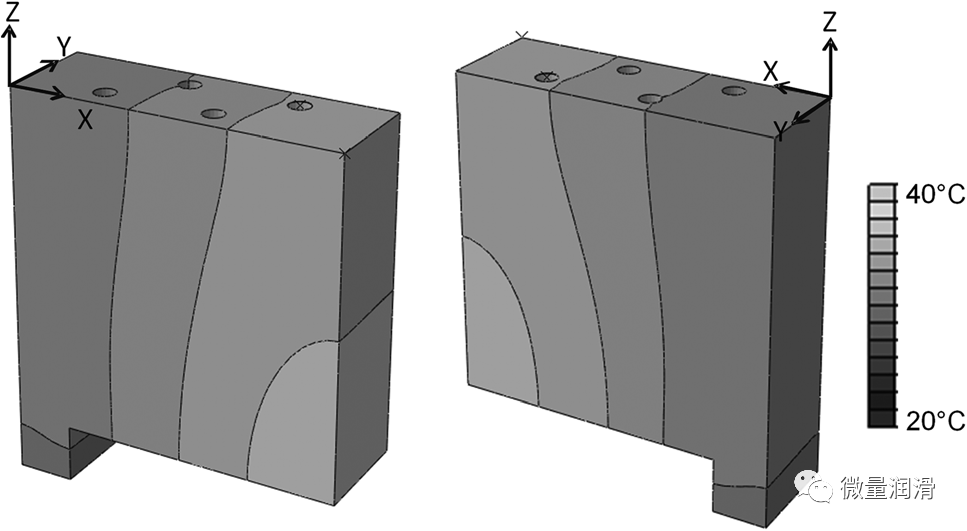
圖14.    4號鉆孔鉆孔結(jié)束后22s內(nèi)工件溫度分布的兩個視角

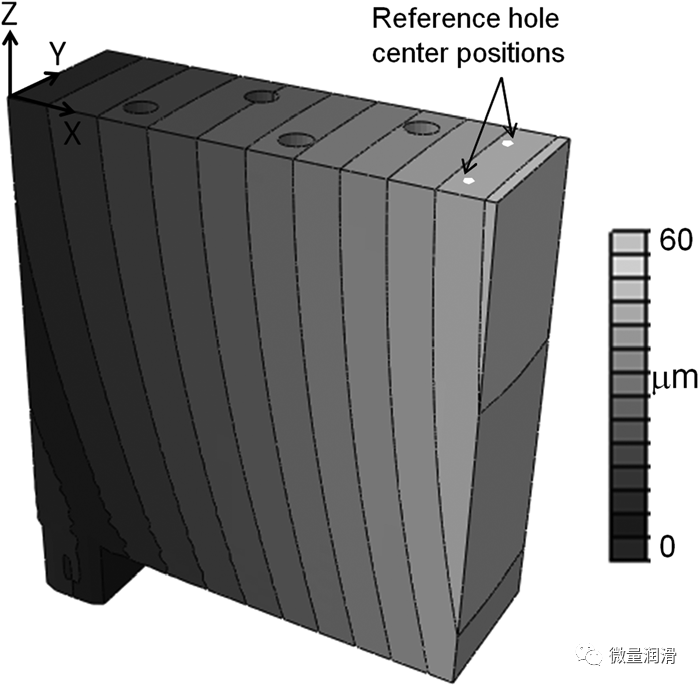
圖15.    參考鉆孔開始時的工件變形

有限元模型預(yù)測，兩組參考孔（c和d相對于a和b）之間的熱膨脹為51lm。潛在的測量誤差為10lm，與實(shí)驗測量的61lm相當(dāng)，驗證了所提出的FEA三維熱載體和熱變形模型，用于預(yù)測MQL深孔鉆孔工件熱變形。

6、    結(jié)論

本研究提出了熱載體模型，并實(shí)驗驗證了預(yù)測三維工件溫度分布和熱畸變。該方法在研究MQL多孔鉆孔的熱變形方面具有實(shí)用的、通用的、計算時間效率的和可行的方法。該方法可用于設(shè)計夾緊布局，以減少熱變形，選擇加工參數(shù)，以及在MQL加工操作中的誤差補(bǔ)償，以提高零件精度。假設(shè)該熱變形模型的熱通量在每個鉆孔中都是可重復(fù)的。鉆頭磨損和鉆力、扭矩和熱通量的逐漸增加的影響可以納入未來的研究。

在熱載體模型中，在鉆孔前去除整個孔的方法將去除在鉆孔期間可能傳導(dǎo)到工件上的一些熱量。如果孔間的距離較大或鉆機(jī)進(jìn)料率相對于工作材料的熱擴(kuò)散相對較快，則與該方法相關(guān)的誤差是有限的。為了最小化這個潛在的誤差，一個深孔可以被分成幾個段，然后依次去除。本研究研究了這種逐步去除的方法，將每個孔劃分為三個深度相同的節(jié)段。四個孔的12個段被去除，熱載體依次插入每個段。例如，圖。16(a)顯示了2孔的第一段，熱載體在這段中間。圖16(b)和16(c)分別顯示了在進(jìn)一步插入熱載體后，對#2孔的第二和第三段的去除。A、B和C點(diǎn)溫度的初始方法和階梯去除方法之間的差異。9)4號鉆孔后22s，僅為0.3%。這證實(shí)了在本研究中不需要逐步去除的方法。

附錄

在第三章節(jié)中，給定實(shí)例的總吸熱量的計算方法為

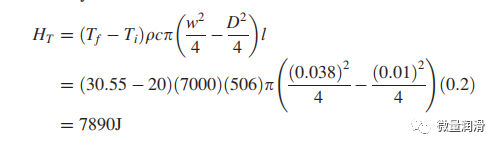
其中，Tf為最終穩(wěn)態(tài)溫度，Ti為初始工件溫度。w和D分別為工件和鉆孔（孔）的直徑，q和c分別為工件密度和比熱。HWS熱流所貢獻(xiàn)的熱量由

其中t是時間，x是沿孔的軸向位置?？倳r間tf為50s，總深度l為0.2m。